Lab 10
Objectives
- Learn a basic algorithm for sorting a list
- Learn something about measuring performance
In this lab you are going to implement a sorting algorithm and then put it through its paces to see how it performs.
Part 0: Getting started
There is no starter code this week, so you can just create a new file called lab10.py.
Part 1: Learn the algorithm
A great deal of time and energy has been put into developing good sorting algorithms, so there are a lot of them out there. We are going to take a look at one of the easier to understand algorithms called Selection Sort.
To understand this algorithm, imagine that we have partially sorted it. We have a dividing line and the elements on the left of the line are where they belong and the items on the right side are unsorted.
We will look through all of the unsorted elements looking for the smallest one. We then swap the smallest item with the element at the start of the unsorted portion of the list. That element is now where it belongs, so we can move the dividing line forward by one. We continue doing this until the whole list is sorted.
In truth, an easier way to think about this is instead of a dividing line, we can think of it as the cell that we want to find the correct value for.
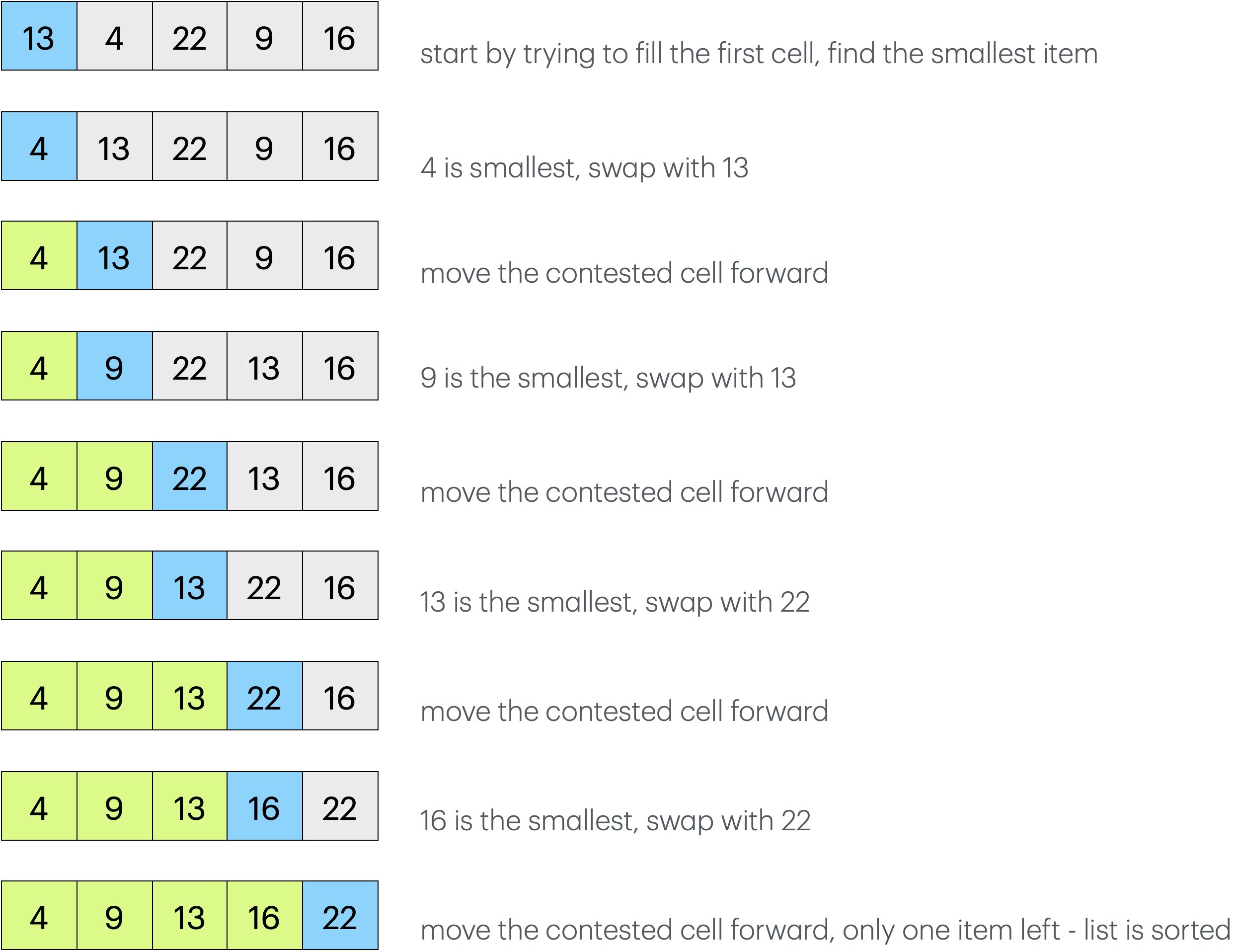
Now that you have an idea about how the algorithm works, go find a portion of white board and do it for yourselves. Write out five random(ish) numbers. Walk through the steps. Think about how you would implement this. To help yourselves out, write the indices above your list. Create some variables to keep track of where you are like you were a computer.
Part 2: Implement the algorithm
Create a new function called selection_sort that takes in a single parameter, a list of values called lst. The function should sort the list in place and then return the list. Note that returning the list is a useful, but not necessary step (though it is for you) since the list is sorted in place.
selection_sort
|
|||
|---|---|---|---|
| Parameters |
|
||
| Return type |
list
|
||
Steps
- Step 1: Create a function called
selection_sortwith parameterlst. Don’t forget your docstring! - Step 2: Create a
forloop that iterates over the indices of the list. This will provide the index of the currently contested cell. It can stop one shy from the end of the list since there is nothing to do for the last cell. - Step 3: Create a new variable to store the location of the smallest element in the unsorted list. Set it equal to the current cell.
- Step 4: Create a nested for loop that visits all of the unsorted cells. If you find a smaller value than the one you are currently marking with your new variable, update the variable to the new location.
- Step 5: Outside of the inner loop, swap the values of the contested cell and the location of the smallest unsorted value.
- Step 6: Outside of both loops, return the list
- Step 7: Test your new sorting algorithm on some short lists
- Step 8: Call one of us over to check if your algorithm lhas the correct implementation
Part 3: Setting up to experiment on the algorithm
Now that you have a sorting algorithm, we want to see how it performs. To do that, we need two more functions.
The first function should just generate lists of random numbers. You can make random lists by hand, but we want BIG lists.
Wrote a function called make_random_list, which takes in a single argument called count. It should return a list of length count of random integers between 0 and count. You should use random.randint to generate the values (after you import random). Don’t forget the doctring!
make_random_list
|
|||
|---|---|---|---|
| Parameters |
|
||
| Return type |
list
|
||
Steps
At this point you should be able to write a loop to generate a list of random numbers, so you are on your own here…
The second function you should write will time your function and compare its run time to the built-in sort method for comparison. We will call the function time_sort and it take in the list we want to try sorting (lst).
The function will return a tuple. The first element should be the time taken for selection sort, and the second should be the time taken by the built-in sort algorithm.
The actually timing will be done with the help of the time module (which you have seen in class before). We will use time.perf_counter() which returns an accurate number of seconds from some unspecified point in the past. To time the duration of a task, we call time.perf_counter() before the task and store the value. Then we call it again after the task and subtract the first time from the new one to get the elapsed time between the two events.
time_sort
|
|||
|---|---|---|---|
| Parameters |
|
||
| Return type |
tuple two floats
|
||
Steps
- Step 1: Import the
timemodule at the top of the file. - Step 2: Create a new function called
time_sort. It should take a single argument:lst. Add your docstring. - Step 3: Your computer is not completely ideal, so the time can vary from run to run. To compensate, we are actually going to sort the list 5 times and average the times together. So, start by making a value to store the accumulated times.
- Step 4: Make a
forloop that runs five times. - Step 5: One problem with running these kinds of tests is that once the list is sorted, further attempts to sort it will be working with different data. So, we want to sort a copy of the list. Use the list’s built-in
copy()function to make a copy of the list inside of yourforloop. - Step 6: Call
time.perf_counter()and store the value. = Step 7: Useselection_sortto sort your list - Step 8: Call
time.perf_counter()and store the value. - Step 9: Subtract the first time from the second time and add the result to your time accumulation variable.
- Step 10: Outside of the loop, divide the accumulated time by 5.
- Step 11: Return the calculated time. Test your function a few times with different list lengths to see how it works.
- Step 12: Now you want to do the same thing for the built in
sortmethod. Copy your loop and time accumulation variable and paste it underneath the existing loop. - Step 13: Rename the time accumulation variable everywhere it appears in this new block of code.
- Step 14: Replace the call to
selection_sortwith a call to your list’s built insort()method. - Step 15: Change the return value to be a tuple that includes the time for
selection_sortin the first cell and the time for the built-insortin the second.
- Step 16: Test you function.
Part 4: Experimentation
For the final part of the lab, you are going to run a couple of experiments. So we know that you ran them, we would like you to add a variable called experiments to your file above the functions. experiments will be a dictionary that holds the results of your experiments. The keys of this dictionary will be listed below. The values should be the tuples returned by running the experiment associated with the key in the table below.
| Key | Experiment |
|---|---|
"50 unsorted" |
sort an unsorted list of 50 items |
"50 sorted" |
sort an already sorted list of 50 items |
"500 unsorted" |
sort an unsorted list of 500 items |
"500 sorted" |
sort an already sorted list of 500 items |
"5000 unsorted" |
sort an unsorted list of 5000 items |
"5000 sorted" |
sort an already sorted list of 5000 items |
Yes, some of these experiments are asking you to run the experiment on a list that is already sorted. What happens when you try to sort a sorted list?
Please run the experiments and paste the resulting tuples into the experiments dictionary rather than trying to get the structure to auto-populate. We want you to look at these values and think about them.
Questions to think about: - What might the big-O complexity of these two sort functions be? - Is there a time difference between the two sorting algorithms? If so, why might that be? - Is there a time difference between trying to sort a sorted list and an unsorted list? If so, why?
We will visit these questions in our next class meeting.
Turning in your work
One you are done, submit lab10.py to gradescope and ensure that you have passed all of the tests. Your file should contain three functions: selection_sort, make_random_list, and time_sort in addition to the experiments dictionary. Each function should have a docstring.