Homework Six
Due 2025-04-10 at the start of class
Submit on GradescopeObjectives
- Demonstrate your ability to convert from binary representation to decimal value
- Demonstrate your ability to convert from decimal values to representations in other bases
- Demonstrate your ability to create sound
- Demonstrate your ability to manipulate sound
Getting started
For this assignment, we have another four functions for you to write. Please pay attention to all of these instructions. Even this front matter, which may look the same (and many of you skip over) has changed.
For this assignment, there is no starter code – so create a new file called homework06.py for your work.
Feel free to work through the functions in any order. Whatever order you use, we suggest that you take the time to test each one as you go rather than trying to write all four out like they were part of an essay and then testing at the very end. Treat these are four totally separate and distinct problems (which they are).
Submit your solution on Gradescope using the button above. Feel free to resubmit as your complete each problem to check your progress. To repeat – you only need to submit homework06.py.
Sounds
Two of these problems deal with sound. Make sure you have read through Working with Sound and have the midd_media package installed.
Python subset
For this assignment, the allowed subset varies from problem to problem. Be sure to read each problem carefully.
Satisfactory vs. Excellence
A solution for these questions that is excellent will have the all of the following qualities
Style
An excellent function will have a docstring that is formatted in the way shown in the lectures. It should include:
- the purpose of the function
- the type and purpose of each parameter (if any)
- the type and meaning of the output (if any)
In addition, you should follow some of the PEP8 guidelines on whitespace. The ones we will be looking at are:
- no whitespace between names and
(or[(e.g.,f (5)should bef(5)ands [3:5]should bes[3:5]) - there should be a single space around operators (e.g.,
x=4+1should bex = 4 + 1andy = 3 -2should bey = 3 - 2) - there should be a space after commas, but not before (e.g.,
f(4 , 5)orf(4,5)should bef(4, 5))
Special cases and requirements
For some of the problems, we have identified special cases or requirements that we have deemed potentially more challenging and not essential to a satisfactory solution. An excellent solution will cover all cases. These cases will be identified in the autograder by tests with * at the end of the title (so make sure you submit frequently as you are working).
Problem 1: Convert from binary
Write a recursive function called from_binary. It should take in a string (binary_str) containing a binary representation of a value. It should output the integer value of the representation. You may assume that the string will consist solely of “0”s and “1”s. The only function call you are allowed (other than any recursive calls) is to len (not even len is required to solve the problem).
from_binary
|
|||
|---|---|---|---|
| Parameters |
|
||
| Return type | int | ||
Examples
>>> from_binary("0")
0
>>> from_binary("1")
1
>>> from_binary("10")
2
>>> from_binary("101010")
42
>>> from_binary("1111")
15Problem 2: Converting to other bases
Write a function called dec_to_base that takes in a positive integer num and an integer larger than 1 called base. The function should return a string representation of the input num in the specified base. You can assume that num will be positive and that the base will be between 2 and 36 (inclusive). For digits beyond 9, you should use uppercase letters.
to_base
|
|||||
|---|---|---|---|---|---|
| Parameters |
|
||||
| Return type |
string
|
||||
Examples
>>> dec_to_base(5, 2)
'101'
>>> dec_to_base(42, 16)
'2A'
>>> dec_to_base(42, 8)
'52'
>>> dec_to_base(279, 2)
'100010111'
>>> dec_to_base(279, 4)
'10113'
>>> dec_to_base(12, 20)
'C'
>>> dec_to_base(19, 20)
'J'
>>> dec_to_base(20, 20)
'10'
>>> dec_to_base(279, 36)
'7R'
>>> dec_to_base(11259375, 16)
'ABCDEF'Problem 3: Generate a sawtooth wave
Write a new function called make_sawtooth that generates a new sound. The generated sound should be a sawtooth wave that lasts for duration seconds and at the provided frequency.
The sawtooth is another periodic signal, somewhere between the complexity of the square wave you saw in class and the sine wave you saw in lab. It is typified by ramps that run from the lowest value up to the highest value, and then drop down to the lowest value to do it again.
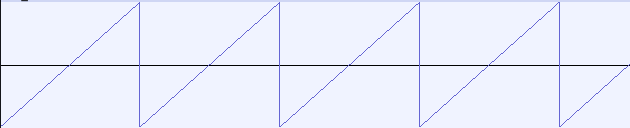
The bounds of the ramp depend our our desired amplitude, but for your ramp, you should range from middsound.MINVALUEto middsound.MAXVALUE. The frequency for the sawtooth wave is the number of complete ramps per second.
As the combination of numeric precision and the fact that the duration and the frequencies may not be whole numbers, you may be in the middle of a ramp when you have reached the expected number of samples. An Excellent solution will finish the current ramp. Even if this overruns the duration slightly, it will be by hundredths or thousandths of a second.
Remember that all samples must be integers that are no larger than middsound.MAXVALUE and no smaller than middsound.MINVALUE.
make_sawtooth
|
|||||
|---|---|---|---|---|---|
| Parameters |
|
||||
| Return type |
middsound.Sound
|
||||
Examples
For the examples, there isn’t a visual output. You need to listen to the sounds. We have included a pair of sawtooth tones for comparison purposes.
Expected outputs
>>> a4 = make_sawtooth(1, 440)
>>> a1 = make_sawtooth(1, 55)
>>> a4.play()
>>> a1.play()Problem 4: Mix sounds
Write a new function called mix_soundsthat mixes two sounds (snd and snd2) together and returns a new Sound with the result. “Mixing” in this context essentially means “adding”. A third parameter, balance determines how much each sound contributes. If the balance is \(0.5\), both sounds contribute equally and are scaled by \(50%\). If the balance is \(0.0\), only snd1 will be heard at full strength. If the balance is \(1.0\), then only snd2 will be heard at full strength. If the balance is set at \(0.75\), then snd1 will be added at \(25%\) strength and snd2 will be added at \(75%\) strength.
For Excellent credit, your function should handle the case where the two sounds are different lengths. In that case, the final sound should contain the full content of both sounds. The shorter sound will stop when it stops and the longer sound will continue on at the strength determined by the balance until it is complete.
Remember that all samples must be integers that are no larger than middsound.MAXVALUE and no smaller than middsound.MINVALUE.
mix_sounds
|
|||||||
|---|---|---|---|---|---|---|---|
| Parameters |
|
||||||
| Return type |
middsound.Sound
|
||||||
Examples
For the examples, there isn’t a visual output. You need to listen to the mix. We have included a collection of sound files used in this example. The ones names with a letter and a name are pure sine tones with the letter indicating the note and octave. These are all two seconds long.
Input files
Expected outputs
>>> a4 = middsound.open("a4.wav")
>>> c5 = middsound.open("c5.wav")
>>> ham = middsound.open("hamster_short.wav")
>>> chord10 = mix_sounds(a4, c5, .10)
>>> chord50 = mix_sounds(a4, c5, .50)
>>> chord90 = mix_sounds(a4, c5, .90)
>>> chord10.play()
>>> chord50.play()
>>> chord90.play()
>>> ham_mix = mix_sounds(ham, c5, 0.5)
>>> ham_mix.play()