Homework Six (retake)

Due 2025-04-26 at 11:59p

Submit on Gradescope

This is your second shot at the problems from Homework Six. If you missed any of the problems, you are strongly advised to try again. Your goal is to complete (Satisfactory or Excellent) up to four problem across Homework Six and this set, but you are encouraged to do more – especially if you were challenged by the first set of problems. Remember that we evaluate each problem individually, so there are no issues if you only do a subset of the problems (including none).

Objectives

• Demonstrate your ability to convert from binary representation to decimal value
• Demonstrate your ability to convert from decimal values to representations in other bases
• Demonstrate your ability to create sound
• Demonstrate your ability to manipulate sound

Getting started

For this assignment, we have another four functions for you to write. Please pay attention to all of these instructions. Even this front matter, which may look the same (and many of you skip over) has changed.

For this assignment, there is no starter code – so create a new file called homework06r.py for your work.

Feel free to work through the functions in any order. Whatever order you use, we suggest that you take the time to test each one as you go rather than trying to write all four out like they were part of an essay and then testing at the very end. Treat these are four totally separate and distinct problems (which they are).

Submit your solution on Gradescope using the button above. Feel free to resubmit as your complete each problem to check your progress. To repeat – you only need to submit homework06r.py.

Sounds

Two of these problems deal with sound. Make sure you have read through Working with Sound and have the midd_media package installed.

Python subset

For this assignment, the allowed subset varies from problem to problem. Be sure to read each problem carefully.

Satisfactory vs. Excellence

A solution for these questions that is excellent will have the all of the following qualities

Style

An excellent function will have a docstring that is formatted in the way shown in the lectures. It should include:

• the purpose of the function
• the type and purpose of each parameter (if any)
• the type and meaning of the output (if any)

In addition, you should follow some of the PEP8 guidelines on whitespace. The ones we will be looking at are:

• no whitespace between names and ( or [ (e.g., f (5) should be f(5) and s [3:5] should be s[3:5])
• there should be a single space around operators (e.g., x=4+1 should be x = 4 + 1 and y = 3 -2 should be y = 3 - 2)
• there should be a space after commas, but not before (e.g., f(4 , 5) or f(4,5) should be f(4, 5))

Special cases and requirements

For some of the problems, we have identified special cases or requirements that we have deemed potentially more challenging and not essential to a satisfactory solution. An excellent solution will cover all cases. These cases will be identified in the autograder by tests with * at the end of the title (so make sure you submit frequently as you are working).

Problem 1: adjust_speed

Write a function called adjust_speed that takes in a sound (snd) and float (speed). The function should return a new sound that has been sped up or slowed down by the factor passed in as speed. So, for example, is speed is 2, the new sound should be twice as fast as the original. If it is 0.5, then the sound should be at half speed. It we set speed to 1, we should get the original sound back.

While conceptually we could do this by tinkering with the framerate, you should do this by changing the sound at the sample level. Ideally, we would resample the original sound at a new rate, but we don’t have access to the original sound. As such, the recommended approach will be to think about the point of time you would like to sample and then grab the sample from the original sound that is closest to that point.

Note that changing the speed will change the pitch. There are fancy algorithms that attempt to change the speed without changing the pitch (or change the pitch without changing the speed). We are not going to do that here.

adjust_speed
Parameters	snd middsound.Sound speed int or float
Return type	middsound.Sound

Examples

Since there is no visual output, we are including some sound files as example output.

• original file (download)
• `adjust_speed(snd, 2) (download)
• `adjust_speed(snd, 0.5) (download)
• `adjust_speed(snd, 1.5) (download)

Problem 2: from_base

Write a recursive function called from_base that takes in a string (num) and an integer (base). The string num holds the representation of a number in the provided base. The function should return the decimal representation of the number. For digits that require letters, your function should handle both upper and lower cases.

You are not expected to handle invalid representations (e.g., "2a" in base 10).

You are permitted the use of the functions upper, lower, len, ord, and chr.

from_base
Parameters	num str base int (valid bases are between 2 and 36 inclusive)
Return type	int

Examples

>>> from_base("101010", 2)
42
>>> from_base("101010", 4)
1092
>>> from_base("101010", 16)
1052688
>>> from_base("2A", 16)
42
>>> from_base("2z", 36)
107
>>> from_base("42", 10)
42

Problem 3: Generate a triangle wave

Write a function called make_triangle that takes two numbers: duration and frequency. The generated sound should be a triangle wave that lasts for duration seconds and at the provided frequency.

The triangle is another periodic signal, similar to the sawtooth. Like the sawtooth, it ramps up from the lowest amplitude to the largest, but it reaches that point at the halfway point of the cycle. It then ramps back down to the lowest amplitude again. Because it doesn’t have the drop-off of the sawtooth, it makes a more pleasant tone than the sawtooth.

Example triangle wave

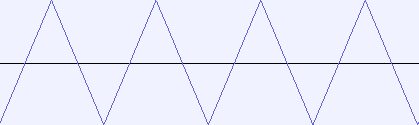
The bounds of the triangle depend our our desired amplitude, but for your triangle, you should range from middsound.MINVALUEto middsound.MAXVALUE. The frequency for the triangle wave is the number of complete triangles per second.

As the combination of numeric precision and the fact that the duration and the frequencies may not be whole numbers, you may be in the middle of a triangle when you have reached the expected number of samples. An Excellent solution will finish the current triangle. Even if this overruns the duration slightly, it will be by hundredths or thousandths of a second.

Remember that all samples must be integers that are no larger than middsound.MAXVALUE and no smaller than middsound.MINVALUE.

make_triangle
Parameters	duration int or float frequency int or float
Return type	middsound.Sound

Examples

Since there is no visual output, we are including some sound files as example output.

• make_triangle(1, 440) (download)
• make_triangle(0.5, 196) (download)
• make_triangle(2, 73.42) (download)

Problem 4: echo

Write a function called echo that takes in a sound (snd) and two numbers (delay and strength) and returns a new sound file that adds an echo effect to the original sound. The delay is the amount of time (in seconds) to wait before the echo starts and the strength is the percentage of the original signal that we will use to form the echo. This number should be less than one. The basic principle behind the echo is that you are hearing a repetition of sound waves that you had heard previously, after they have reflected off some surface. The echo will typically be quieter and will be combined with the other sounds you are currently hearing.

Generating a new sample with an echo: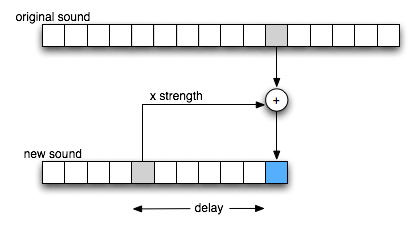

There are three separate phases to building the new sound:

• The first phase looks at the period until the echo starts. For this period, the new sound will be a copy of the original sound.
• The second phase looks at the part of the the new sound that starts where the first part ends and will run until we run out of sample from the original sound. In this part, we add the first echo: our samples should consist of the sum of the original sound (what is happening now) and a scaled version of what happened delay samples earlier in our new sound (why the new sound? because we want the echo to echo as well).
• Finally, you should include a period after the original sound has finished that just consists of the remaining echoes until the sound dies down to zero.

Here is an example for an echo where we have delayed two samples and have an echo with a strength of 50%.

Example echo

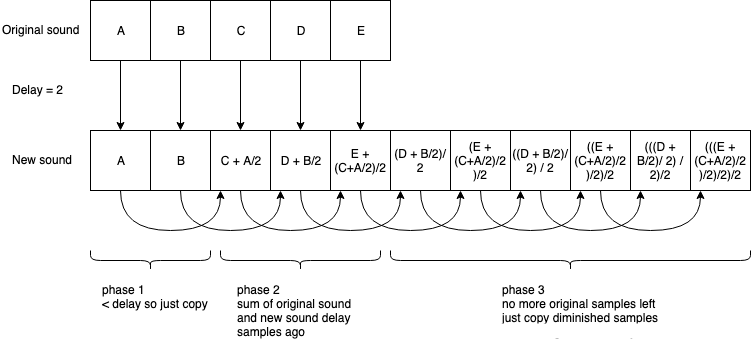
The challenge here is determining that the sound has actually diminished down to zero. Since our sound is recording changing values, a sample of zero could be found in the middle of a very loud sound. We want the value to be zero, and the have been zero, for some time. The only way to be properly sure that this is not the sound swinging past zero, or just the middle of a quiet part of the sound, is to wait for the length of the original sound. So, you can stop adding samples to the new sound and return it once you have appended enough continuous zeros to equal the length of the original sound.

echo
Parameters	snd middsound.Sound delay int or float strength float (should be a value that is greater than 0 and less than 1)
Return type	middsound.Sound

Examples

Since there is no visual output, we are including some sound files as example output.

• original file (download)
• echo(snd, .25, .75) (download)
• echo(snd, 1.0, .4) (download)
• echo(snd, .05, .25) (download)