Homework Nine
Due 2025-05-01 at the start of class
Submit on GradescopeObjectives
- Demonstrate your ability to create a class
- Demonstrate your ability to add methods to a class
- Demonstrate your ability to create a system of connected classes
Getting started
For this assignment, there are still four parts, but it is not neatly packaged together as four separate functions. You will be writing classes, and as a result, you will write more functions (methods), but they are simpler.
In addition, the problems are paired up, so problems one and two are linked, as are three and four. You can still skip around and focus on what you want, but problem one should be done before two and three should be done before four.
There is no starter code this time, so create a new file and call it homework09.py.
Submit your solution on Gradescope using the button above. Feel free to resubmit as you complete each problem to check your progress. To repeat – you only need to submit homework09.py.
Python subset
For this assignment, we have not placed any restrictions on what you may use.
Satisfactory vs. Excellence
A solution for these questions that is excellent will have the all of the following qualities
Style
An excellent function will have a docstring that is formatted in the way shown in the lectures. It should include:
- the purpose of the function
- the type and purpose of each parameter (if any)
- the type and meaning of the output (if any)
In addition, you should follow some of the PEP8 guidelines on whitespace. The ones we will be looking at are:
- no whitespace between names and
(or[(e.g.,f (5)should bef(5)ands [3:5]should bes[3:5]) - there should be a single space around operators (e.g.,
x=4+1should bex = 4 + 1andy = 3 -2should bey = 3 - 2) - there should be a space after commas, but not before (e.g.,
f(4 , 5)orf(4,5)should bef(4, 5))
Special cases and requirements
For some of the problems, we have identified special cases or requirements that we have deemed potentially more challenging and not essential to a satisfactory solution. An excellent solution will cover all cases. These cases will be identified in the autograder by tests with * at the end of the title (so make sure you submit frequently as you are working).
Problem 1: Rect
Create a new class called Rect. The class should have four properties: - x - the \(x\) location of the upper left hand corner of the rectangle - y - the \(y\) location of the upper left hand corner of the rectangle - width - the width of the rectangle - height - the height of the rectangle
These should be initialized in the constructor.
The class should also have three methods in addition to (__init__):
__repr__()- returns the representation of the rectanglearea()- returns the area of the rectangleaspect_ratio()- returns the aspect ratio of the rectangle
The representation of the rectangle should be a string of the form "Rect(x, y, width, height)" (with the values filled).
The aspect ratio of a rectangle is the \(\frac{width}{height}\).
Rect
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| Properties |
|
||||||||
Rect.__init__
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameters |
|
||||||||
Rect.__repr__
|
|
|---|---|
| Return type |
str
|
Rect.area
|
|
|---|---|
| Return type |
int or float
|
Rect.aspect_ratio
|
|
|---|---|
| Return type |
float
|
Examples
>>> r1 = Rect(5, 5, 10, 20)
>>> r1
Rect(5, 5, 10, 20)
>>> r1.area()
200
>>> r1.aspect_ratio()
0.5
>>> r2 = Rect(6, 2, 25, 5)
>>> r2
Rect(6, 2, 25, 5)
>>> r2.area()
125
>>> r2.aspect_ratio()
5.0Problem 2: Rect intersections
For this problem, you are going to add a new method to the Rect class.
The method is intersection, which will take in a Rect object (rect) and return a new Rect that describes the region overlapped by both rectangles. If the two rectangles do not overlap, then the method should return None
To achieve a score of “Excellent”, your function should work for negative dimensions as well as positive.
Rect.intersection
|
|||
|---|---|---|---|
| Parameters |
|
||
| Return type |
Rect (or None)
|
||
Examples
>>> r1 = Rect(10, 10, 15, 20)
>>> r2 = Rect(5, 5, 15, 10)
>>> r1.intersection(r2)
Rect(10, 10, 10, 5)
>>> r3 = Rect(15, 12, 5, 8)
>>> r1.intersection(r3)
Rect(15, 12, 5, 8)
>>> r4 = Rect(15, 20, 30, 5)
>>> r1.intersection(r4)
Rect(15, 20, 10, 5)
>>> r5 = Rect(30, 5, 50,50)
>>> r1.intersection(r5)Problem 3: drawing part 1
The overall goal of this part of the assignment is to write some classes that will allow us to draw some more complicated shapes with the turtle (without using recursion). In part 1, you will create two new classes: Point and Segment.
There are some requirements for how you should use turtle to get it to play nice with the autograder. First, when you import turtle, do so by writing import turtle at the top of your file. Second, you may only use the following turtle functions:
turtle.gototurtle.dotturtle.penupturtle.pendown
The Point Class
You’ll start with Point, which should have two properties:
x- the \(x\) position of the pointy- the \(y\) position of the point
The constructor should take two arguments (x and y) and initialize the properties.
The class should also have three methods in addition to (__init__):
scale()- takes one argument in addition toself(factor) and scales thexandyattributes by the value of factor. In other words, thexandyattributes are both multiplied by this scaling factortranslate()- takes two arguments in addition toself(txandty) and adds these values to thexandyattributes.draw(): takes one Boolean argument in addition toself(withdots) and moves the turtle from wherever it might be to the location identified by thexandyattributes (see turtle.goto()). It also draws a dot (seeturtle.dot()) ifwithdotsisTrue.
Point
|
|||||
|---|---|---|---|---|---|
| Properties |
|
||||
Point.scale
|
|||
|---|---|---|---|
| Parameters |
|
||
| Return type |
None
|
||
Point.translate
|
|||||
|---|---|---|---|---|---|
| Parameters |
|
||||
| Return type |
None
|
||||
Point.draw
|
|||
|---|---|---|---|
| Parameters |
|
||
| Return type |
None
|
||
Examples
>>> p = Point(10, 20)
>>> q = Point(20, 30)
>>> p.scale(5)
>>> p.x
50
>>> p.y
100
>>> q.translate(15, 25)
>>> q.x
35
>>> q.y
55
>>> p.draw(False)
>>> q.draw(True)After these commands, there should be a line from (0, 0) (where the turtle started) to (50, 100), another line from (50, 100) to (35, 55) and a dot at (35, 55). The dot should only be at (35, 55).
The Segment Class
Our shapes will be a collection of segments. In our drawings segments are any sequence of points.
The Segment class will have an attribute that stores a list of points that form the segment (similar to the Deck class storing a bunch of instances of the Card class from Tuesday’s lecture).
Segment should have one property:
points: a list ofPointobjects that form a segment. We will provide you sample segments but, if you want to create your own shapes, keep in mind that a line segment will be drawn between to consecutive points so, when you draw your segment, make sure you put your points in the correct order. In your__init__method, you should store the points in thepointsattribute.
The constructor should take one argument (points) and initialize the property.
The class should also have one method in addition to (__init__):
draw(): takes one Boolean argument in addition toself(withdots) and draws the segment by iterating through the list ofPointobjects stored in thepointsattribute and calling thedrawmethod for each of the points passing thewithdotsvariable as argument. Before drawing your first point, you should make sure to lift your pen up (turtle.penup()) so that you don’t draw a line between the origin and your first point. Between drawing all of the other points in the segment, your pen should be down (turtle.pendown()). Hint: draw a point by calling tha point’sdraw()method.
The following figure might help clarify the cascading relationship between the draw method for a Segment and the draw method for a Point:
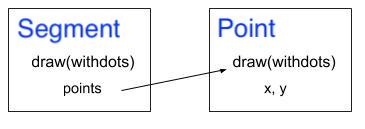
Segment
|
|||
|---|---|---|---|
| Properties |
|
||
Segment.draw
|
|
|---|---|
| Return type |
None
|
Examples
>>> p0 = Point(100, 100)
>>> p1 = Point(200, 100)
>>> p2 = Point(200, 200)
>>> p3 = Point(100, 200)
>>> points = [p0, p1, p2, p3, p0]
>>> segment = Segment(points)
>>> segment.draw(True)You should see a square with side length of 100! Notice that we need to include the initial point p0 at the end of the list of points since we want the segment to close in on itself. There should be a dot at every point since we passed True to the draw function.
Problem 4: drawing part 2
We can now create more complex shapes by introducing a Shape class, which simply stores a collection of Segment objects.
Shapes are stored in files as sequences of segments separated by “Break” (the actual word) that indicates the end of a segment and the beginning of a new one.
Between breaks, segments are represented by a sequence of x- and y-coordinates of a point. For example:
x1 y1
x2 y2
.
.
.
xn yn
Break
x1 y1
x2 y2
.
.
.
xm ym
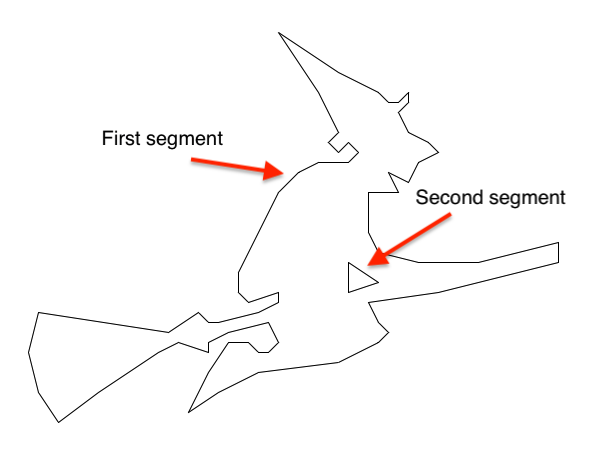
BreakTake a look at a sample file with a shape made of a single segment: witch0.txt. You will notice that there is only one “Break” in this file (one single segment). A slightly more refined version (witch.txt) has two segments (two “Break”): the first segment contains n points and the second segment contains m points. If you look at other examples below, you might see that they are made of many more segments.
Your Shape class should have the following attributes:
segments: list ofSegmentobjects (very similar to what you did for the points inside the segments)
It should also have the following methods:
__init__(): takes one argument in addition toself(a string with the name of a file) and opens that file, reads its content, and stores the points into separate segments. You will have to find out where the “Break”s are so that you can create segments and assign points to them.scale(): takes one argument in addition toself(factor) and scales thexandyattributes of every point of every segment by factor using the pointscalemethod.translate(): takes two arguments in addition toself(txandty) and adds these values to the x and y attributes of every point of every segment using the pointtranslatemethod.draw(): takes one Boolean argument in addition toself(withdots) and calls thedrawmethod for every segment object passing the argumentwithdotsto it. We encourage you to start testing your code using the single segment (provided in thewitch0.txtsample).
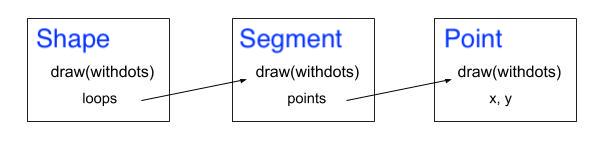
Again, note the cascading relationship between the draw() method for a Shape, the draw() method for a Segment, and the draw() method for a Point. Whatever is passed as the variable withdots into the Shape draw() method, is also passed to draw() for a Segment and, hence, draw() for a Point:
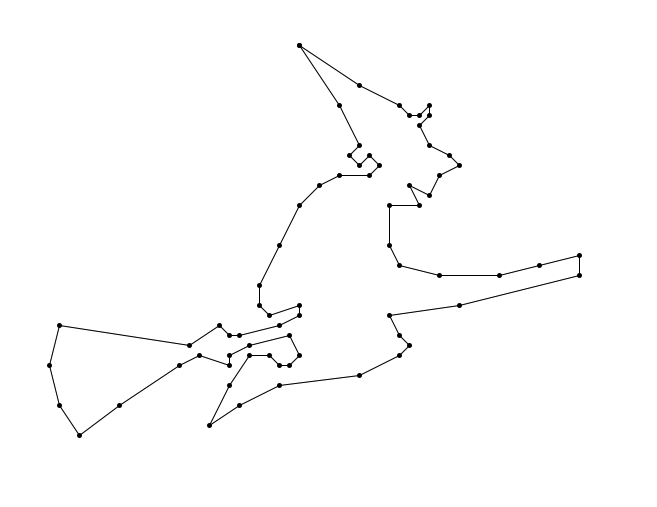
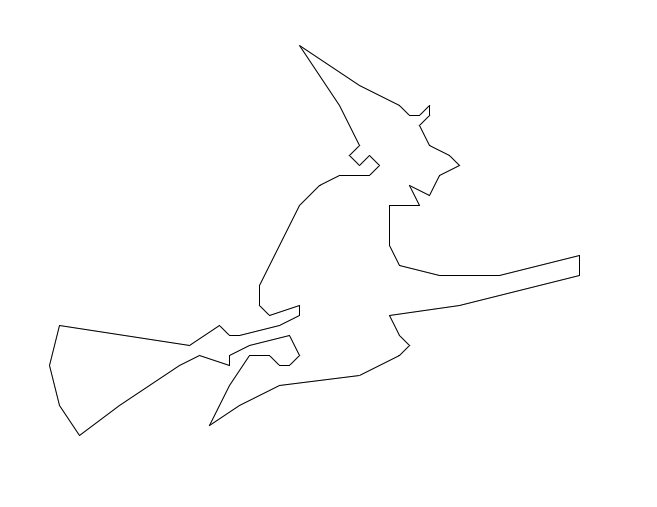
Here are some examples with the witch0.txt file. The witch0.txt file contains a single segment describing the outline of a witch. On the left, this outline is drawn with the withdots option as True. On the right, the withdots options is set to False.
Now onto shapes with multiple segments! If you have multiple segments, every time you encounter the “Break” word in the file, you will need to append the current segment to the segment attribute in the Shape class and instantiate a new segment to store the next set of points.
The images below contain several segments:

Shape
|
|||
|---|---|---|---|
| Properties |
|
||
Shape.scale
|
|||
|---|---|---|---|
| Parameters |
|
||
| Return type |
None
|
||
Shape.translate
|
|||||
|---|---|---|---|---|---|
| Parameters |
|
||||
| Return type |
None
|
||||
Shape.draw
|
|||
|---|---|---|---|
| Parameters |
|
||
| Return type |
None
|
||
Examples
Test your code out by instantiating a shape, and then calling it’s draw method.
>>> witch = Shape('witch0.txt')
>>> witch.scale(20)
>>> witch.translate(500, 0)
>>> witch.draw(True)Play around with some of the sample files:
- blackp.txt
- yoda.txt
- steve.txt
- bunny.txt
- cat.txt
- mike.txt
- jackolantern.txt
- witch0.txt (single-segment witch)
- witch.txt (witch with two segments)
- mystery.txt
Feel free to make your own points files as well and share them on campuswire!