import torch
torch.manual_seed(1234)
def perceptron_data(n_points = 300, noise = 0.2):
y = torch.arange(n_points) >= int(n_points/2)
X = y[:, None] + torch.normal(0.0, noise, size = (n_points,2))
X = torch.cat((X, torch.ones((X.shape[0], 1))), 1)
return X, y
X, y = perceptron_data(n_points = 300, noise = 0.2)Linear Models, Perceptron, and Torch
In this warmup, you will introduce yourself to the model template code that we’ll use to implement several different machine learning models in this course. As you do so, you’ll use the Torch package (instead of Numpy) for numerical calculations.
Here’s a function which generates the kind of data we are going to use with the perceptron, including a feature matrix and a set of predictor labels. Instead of np.arrays, these are now torch.Tensors. You can still think of them as arrays of numbers with most of the same operations. Most things that you have learned about np.arrays will still work for torch.Tensors, and in this warmup I will point out all the relevant differences.
Here’s how it looks:
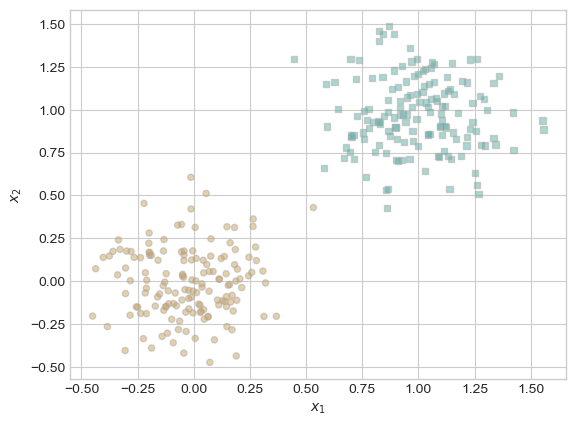
To define a classifier for this data, we are going to define three Python classes.
- The
LinearModelclass is a template for several linear models that we will implement in this class. Recall that a linear model is a model that works by computing a score for each data point like \(s_i = \langle \mathbf{w}, \mathbf{x}_i \rangle\). This class has a single instance variable: the weight vector \(\mathbf{w}\). - The
Perceptronclass inherits from LinearModeland describes the specific linear model we will use in lecture today. - The
PerceptronOptimizerclass will implement the specific learning algorithm that will improve the value of \(\mathbf{w}\) in order to optimize an objective.
Here are the three classes. I have written docstrings for the methods that we’ll implement in this warmup.
class LinearModel:
def __init__(self):
self.w = None
def score(self, X):
"""
Compute the scores for each data point in the feature matrix X.
The formula for the ith entry of s is s[i] = <self.w, x[i]>.
If self.w currently has value None, then it is necessary to first initialize self.w to a random value.
ARGUMENTS:
X, torch.Tensor: the feature matrix. X.size() == (n, p),
where n is the number of data points and p is the
number of features. This implementation always assumes
that the final column of X is a constant column of 1s.
RETURNS:
s torch.Tensor: vector of scores. s.size() = (n,)
"""
if self.w is None:
self.w = torch.rand((X.size()[1]))
# your computation here: compute the vector of scores s
pass
def predict(self, X):
"""
Compute the predictions for each data point in the feature matrix X. The prediction for the ith data point is either 0 or 1.
ARGUMENTS:
X, torch.Tensor: the feature matrix. X.size() == (n, p),
where n is the number of data points and p is the
number of features. This implementation always assumes
that the final column of X is a constant column of 1s.
RETURNS:
y_hat, torch.Tensor: vector predictions in {0.0, 1.0}. y_hat.size() = (n,)
"""
pass
class Perceptron(LinearModel):
def loss(self, X, y):
"""
Compute the misclassification rate. A point i is classified correctly if it holds that s_i*y_i_ > 0, where y_i_ is the *modified label* that has values in {-1, 1} (rather than {0, 1}).
ARGUMENTS:
X, torch.Tensor: the feature matrix. X.size() == (n, p),
where n is the number of data points and p is the
number of features. This implementation always assumes
that the final column of X is a constant column of 1s.
y, torch.Tensor: the target vector. y.size() = (n,). The possible labels for y are {0, 1}
HINT: You are going to need to construct a modified set of targets and predictions that have entries in {-1, 1} -- otherwise none of the formulas will work right! An easy to to make this conversion is:
y_ = 2*y - 1
"""
# replace with your implementation
pass
def grad(self, X, y):
pass
class PerceptronOptimizer:
def __init__(self, model):
self.model = model
def step(self, X, y):
"""
Compute one step of the perceptron update using the feature matrix X
and target vector y.
"""
passPart A
Open a fresh Jupyter notebook with the ml-0451 kernel. Paste in the code that generates the data, as well as the three class definitions above.
Please implement LinearModel.score() and LinearModel.predict() according to their supplied docstrings.
An ideal solution will use no for-loops. It is possible to complete LinearModel.score() with one additional line of code and LinearModel.predict() with two lines of code.
Part B
Please implement Perceptron.loss() according to its supplied docstring. It is possible to complete this function with two lines of code.
Hints
- Two numbers \(a\) and \(b\) have the same sign iff \(ab > 0\).
- In
torch, you can’t compute a.mean()if ais a boolean tensor. Instead, you need to cast ato a tensor of numerical values. One way to do this is by computing (1.0*a).mean().
Check
Once you have completed Parts A and B, the below code should run and the value of l should be 0.5. Paste it into a new cell in your notebook and run it to check.
p = Perceptron()
s = p.score(X)
l = p.loss(X, y)
print(l == 0.5)There are several other methods in these classes that we will need to implement in order to have a functioning classification algorithm, but we won’t worry about those until later.
© Phil Chodrow, 2025