Introduction
Suppose that we have a row of \(n\) parking spaces. An urban planner with a mathematical hobby has asked the following question:
If all cars take up one parking space, and all trucks take up two parkings paces, how many ways are there to fill a row of \(n\) parking spaces with cars and trucks?
For example, here are the 5 ways to fill a row of 4 parking spaces with cars and trucks.
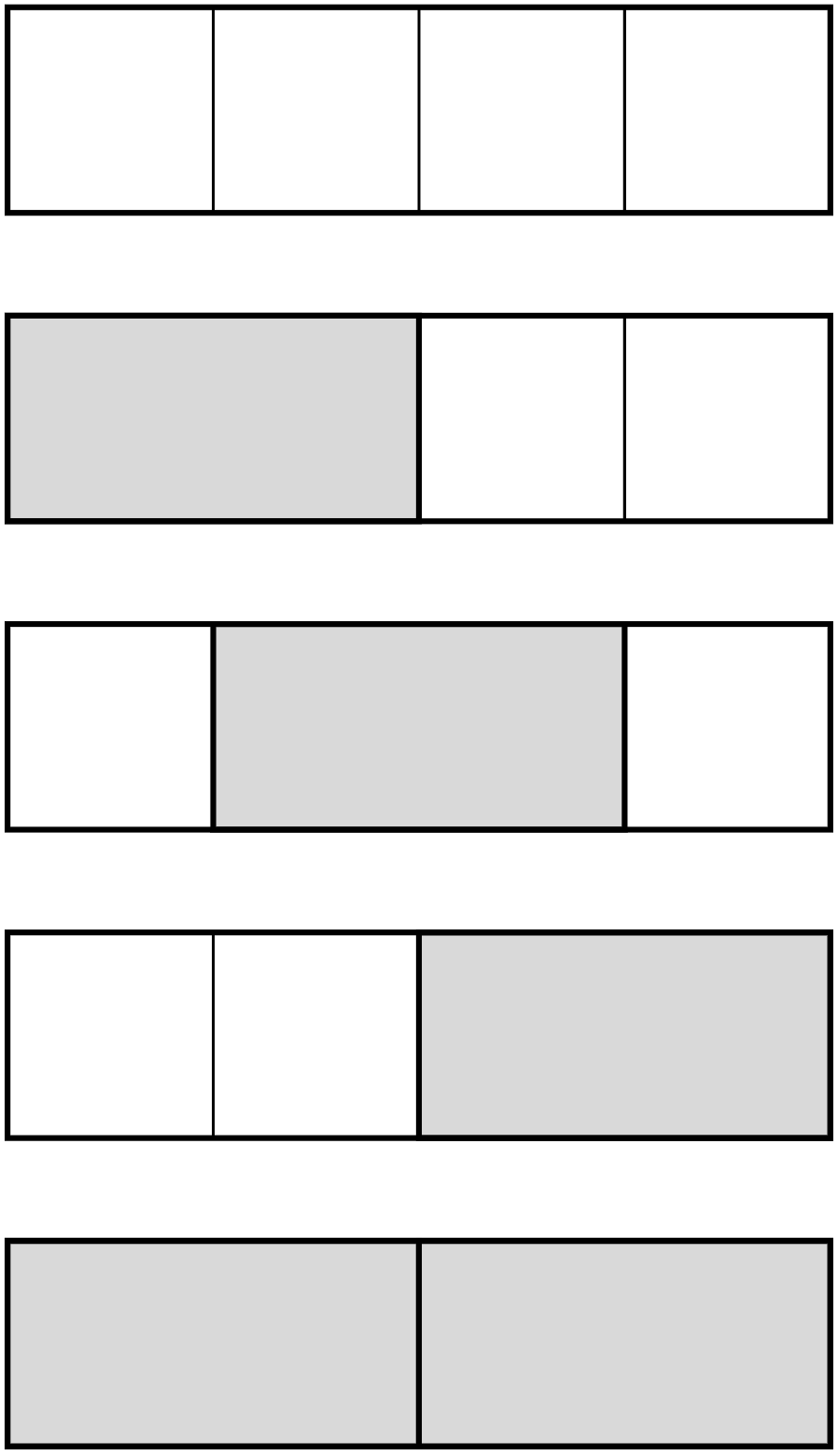
If we let \(P_n\) describe the number of ways to fill \(n\) parking spaces with cars and trucks, this illustration shows that \(P_4 = 5\).
Part A
Draw pictures to compute the values of \(P_1\), \(P_2\), and \(P_3\).
Part B
Make a guess about the value of \(P_n\) for any \(n\) in terms of a sequence we’ve seen before in this class.
Part C
Let’s see if we can prove your guess. Consider a row of \(n \geq 3\) parking spaces. The first space can be occupied by either a car or a truck (which then also occupies the second space). In either case, there is some number of ways to fill in the remaining spaces.
- How many ways are there to fill in the remaining spaces if the first space is occupied by a car?
- How many ways are there to fill in the remaining spaces if the first space is occupied by a truck?
- Combine these two results in order to obtain a recurrence relation for \(P_n\). You should choose between the principles of multiplication and addition.
Part D
Use a combinatorial proof to prove the following theorem: for all \(n \geq 1\),
\[ \begin{aligned} P_n^2 + P_{n+1}^2 = P_{2n+2}\;. \end{aligned} \]
Remember that in a combinatorial proof, you don’t do much algebra! Instead, you just argue that both sides of the equation are different methods of counting the number of ways to do the same thing. In this case, you should count the number of ways to fill a row of \(2n+2\) parking spaces.
Hint: Consider whether or not there is a single truck occupying both of the spaces \(n+1\) and \(n+2\).
© Phil Chodrow, 2024