Lattice Paths
Videos
Yes, there is only one very short video for today.
- Introducing Counting (3:59)
Readings
Please review this chapter, with a special focus on the interpretation of binomial coefficients and lattice path counting. Note that my way of representing a grid in the problems below is different from Levin’s in DMOI, and that will make a difference!
Warmup
Problem 1
Imagine that we are working on a grid with \(n\) rows and \(m\) columns, trying to count the number of paths from the blue dot in the bottom left corner to the orange dot in the top right corner.

The correct formula for the number of paths in this grid is \[ \binom{m + n - k}{m - j} \]
for some mysterious integers \(k\) and \(j\) that do not depend on \(n\) and \(m\). Determine the values of \(k\) and \(j\) and justify your choices.
Problem 2
This time, we still want to get from the blue dot at \((1,1)\) to the orange dot at \((m, n)\). Now, however, there are some walls getting in the way! We are not allowed to cross through any of the grey grid cells.
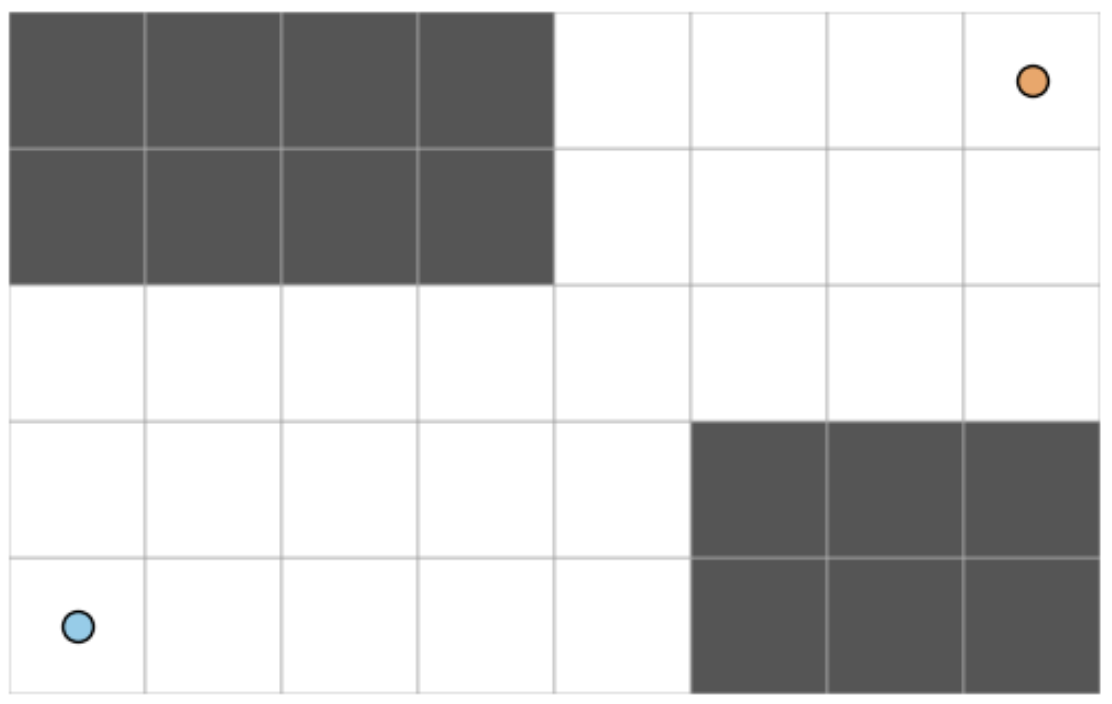
We still want to count the number of ways to get from the blue dot to the orange dot. Consider the following annotated version of the grid in which there is a green dot at the point where the two large rectangular regions intersect:
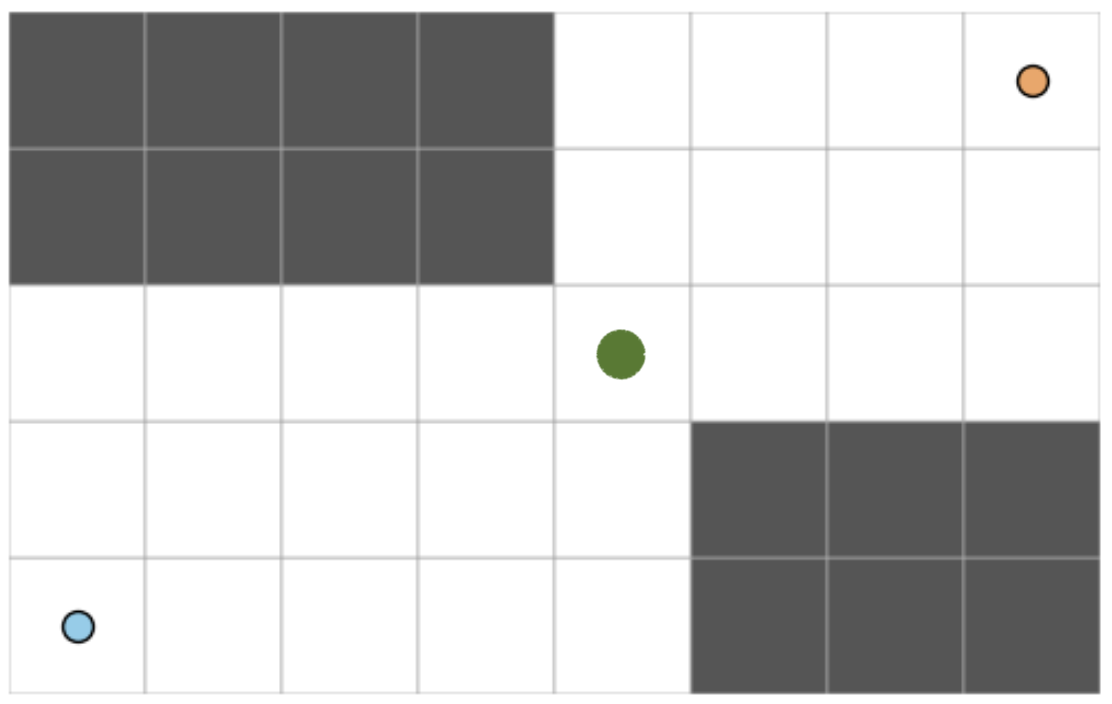
Suppose that this dot is at point \((k, j)\), where \(1 \leq k \leq m\) and \(1 \leq j \leq n\). Give a formula in terms of \(m\), \(n\), \(k\), and \(j\) for the number of paths lattice paths from \((1, 1)\) to \((m, n)\).
Hint: how many paths are there from the blue dot to the green dot? How many paths are there from the green dot to the orange dot? How would we combine these two results to get the solution? Check against the picture to make sure your binomial coefficients line up.
Hint: If you’re struggling to give a general answer, do the problem for the grid shown instead. The orange dot is at \((8, 5)\) and the green dot is at \((5, 3)\).
© Phil Chodrow, 2024